The bitwise operators take operands of integral type that they use as a collection of bits. These operators let us test and set individual bits. As we’ll see in § 17.2 (p. 723), we can also use these operators on a library type named bitset that represents a flexibly sized collection of bits.
As usual, if an operand is a “small integer,” its value is first promoted (§ 4.11.1, p. 160) to a larger integral type. The operand(s) can be either signed or unsigned.
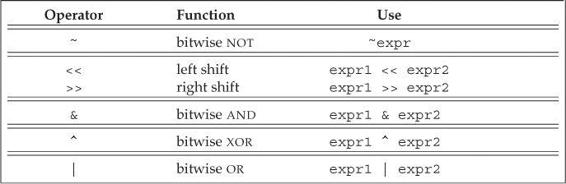
Table 4.3. Bitwise Operators (Left Associative)
If the operand is signed and its value is negative, then the way that the “sign bit” is handled in a number of the bitwise operations is machine dependent. Moreover, doing a left shift that changes the value of the sign bit is undefined.
Because there are no guarantees for how the sign bit is handled, we strongly recommend using
unsignedtypes with the bitwise operators.
We have already used the overloaded versions of the >> and << operators that the IO library defines to do input and output. The built-in meaning of these operators is that they perform a bitwise shift on their operands. They yield a value that is a copy of the (possibly promoted) left-hand operand with the bits shifted as directed by the right-hand operand. The right-hand operand must not be negative and must be a value that is strictly less than the number of bits in the result. Otherwise, the operation is undefined. The bits are shifted left (<<) or right (>>). Bits that are shifted off the end are discarded:

The left-shift operator (the <<
operator) inserts 0-valued bits on the right. The behavior of the right-shift operator (the >>
operator) depends on the type of the left-hand operand: If that operand is unsigned, then the operator inserts 0-valued bits on the left; if it is a signed type, the result is implementation defined—either copies of the sign bit or 0-valued bits are inserted on the left.
The bitwise NOT operator (the ~
operator) generates a new value with the bits of its operand inverted. Each 1 bit is set to 0; each 0 bit is set to 1:

Here, our char operand is first promoted to int. Promoting a char to int leaves the value unchanged but adds 0 bits to the high order positions. Thus, promoting bits to int adds 24 high order bits, all of which are 0-valued. The bits in the promoted value are inverted.
The AND (&), OR (|), and XOR (^) operators generate new values with the bit pattern composed from its two operands:

For each bit position in the result of the bitwise AND operator (the &
operator) the bit is 1 if both operands contain 1; otherwise, the result is 0. For the OR (inclusive or) operator (the |
operator), the bit is 1 if either or both operands contain 1; otherwise, the result is 0. For the XOR (exclusive or) operator (the ^
operator), the bit is 1 if either but not both operands contain 1; otherwise, the result is 0.
It is a common error to confuse the bitwise and logical operators (§ 4.3, p. 141). For example to confuse the bitwise
&with the logical&&, the bitwise|with the logical||, and the bitwise~and the logical!).
As an example of using the bitwise operators let’s assume a teacher has 30 students in a class. Each week the class is given a pass/fail quiz. We’ll track the results of each quiz using one bit per student to represent the pass or fail grade on a given test. We might represent each quiz in an unsigned integral value:
unsigned long quiz1 = 0; // we'll use this value as a collection of bits
We define quiz1 as an unsigned long. Thus, quiz1 will have at least 32 bits on any machine. We explicitly initialize quiz1 to ensure that the bits start out with well-defined values.
The teacher must be able to set and test individual bits. For example, we’d like to be able to set the bit corresponding to student number 27 to indicate that this student passed the quiz. We can indicate that student number 27 passed by creating a value that has only bit 27 turned on. If we then bitwise OR that value with quiz1, all the bits except bit 27 will remain unchanged.
For the purpose of this example, we will count the bits of quiz1 by assigning 0 to the low-order bit, 1 to the next bit, and so on.
We can obtain a value indicating that student 27 passed by using the left-shift operator and an unsigned long integer literal 1 (§ 2.1.3, p. 38):
1UL << 27 // generate a value with only bit number 27 set
1UL has a 1 in the low-order bit and (at least) 31 zero bits. We specified unsigned long because ints are only guaranteed to have 16 bits, and we need at least 17. This expression shifts the 1 bit left 27 positions inserting 0 bits behind it.
Next we OR this value with quiz1. Because we want to update the value of quiz1, we use a compound assignment (§ 4.4, p. 147):
quiz1 |= 1UL << 27; // indicate student number 27 passed
The |= operator executes analogously to how += does. It is equivalent to
quiz1 = quiz1 | 1UL << 27; // equivalent to quiz1 | = 1UL << 27;
Imagine that the teacher reexamined the quiz and discovered that student 27 actually had failed the test. The teacher must now turn off bit 27. This time we need an integer that has bit 27 turned off and all the other bits turned on. We’ll bitwise AND this value with quiz1 to turn off just that bit:
quiz1 &= ~(1UL << 27); // student number 27 failed
We obtain a value with all but bit 27 turned on by inverting our previous value. That value had 0 bits in all but bit 27, which was a 1. Applying the bitwise NOT to that value will turn off bit 27 and turn on all the others. When we bitwise AND this value with quiz1, all except bit 27 will remain unchanged.
Finally, we might want to know how the student at position 27 fared:
bool status = quiz1 & (1UL << 27); // how did student number 27 do?
Here we AND a value that has bit 27 turned on with quiz1. The result is nonzero (i.e., true) if bit 27 of quiz1 is also on; otherwise, it evaluates to zero.

Although many programmers never use the bitwise operators directly, most programmers do use overloaded versions of these operators for IO. An overloaded operator has the same precedence and associativity as the built-in version of that operator. Therefore, programmers need to understand the precedence and associativity of the shift operators even if they never use them with their built-in meaning.
Because the shift operators are left associative, the expression
cout << "hi" << " there" << endl;
executes as
( (cout << "hi") << " there" ) << endl;
In this statement, the operand "hi" is grouped with the first << symbol. Its result is grouped with the second, and then that result is grouped with the third.
The shift operators have midlevel precedence: lower than the arithmetic operators but higher than the relational, assignment, and conditional operators. These relative precedence levels mean we usually have to use parentheses to force the correct grouping of operators with lower precedence.
cout << 42 + 10; // ok: + has higher precedence, so the sum is printed
cout << (10 < 42); // ok: parentheses force intended grouping; prints 1
cout << 10 < 42; // error: attempt to compare cout to 42!
The last cout is interpreted as
(cout << 10) < 42;
which says to “write 10 onto cout and then compare the result of that operation (i.e., cout) to 42.”
Exercises Section 4.8
Exercise 4.25: What is the value of
~'q' << 6on a machine with 32-bitints and 8 bitchars, that uses Latin-1 character set in which'q'has the bit pattern01110001?Exercise 4.26: In our grading example in this section, what would happen if we used
unsigned intas the type forquiz1?Exercise 4.27: What is the result of each of these expressions?
unsigned long ul1 = 3, ul2 = 7;
(a)
ul1 & ul2(b)
ul1 | ul2(c)
ul1 && ul2(d)
ul1 || ul2